Support Vector Machine(SVM)은 classification 문제를 해결하는 지도 학습 모델 중 하나입니다. SVM은 decision boundary라는 데이터 간 경계를 정의함으로써 classification을 수행하고, unclassified된 데이터가 어느 boundary에 떨어지는지를 확인함으로써 해당 데이터의 class를 예측합니다.

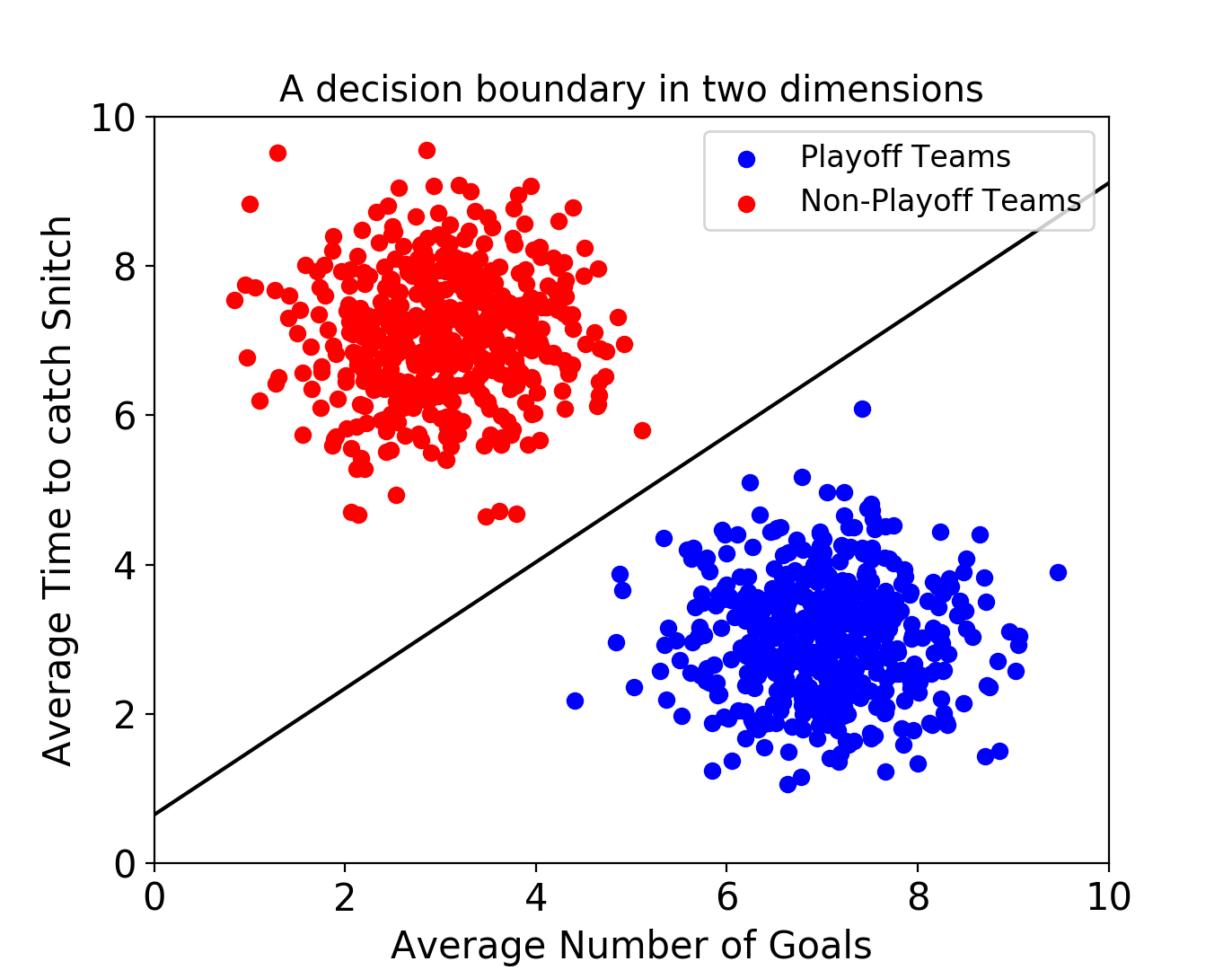
위 그림은 해리포터에 나오는 Quidditch라는 게임 데이터를 재구성하여 SVM으로 분류한 것입니다. 위 모델은 어느 팀이 플레이오프에 진출할지를 예측하고 있습니다. 각 데이터 포인트는 Quidditch 출전팀들의 경기 기록을 나타내고 있고, 이는 평균 골 횟수와 평균 골든 Snitch 캐치 시간으로 나타내집니다.

위와 같이 training set에 대해 검은색 실선으로 decision boundary를 찾은 다음, SVM 모델에 unlabeled 팀 데이터를 전달하여 해당 팀이 플레이오프에 진출 할 수 있을지를 예측할 수 있습니다.

Decision boundary는 세 가지 이상의 피처가 존재할 때에도 존재할 수 있습니다. 만약 위 경우에서 피처가 하나 더 늘어난다면, decision boundary는 평면이 될 것입니다.

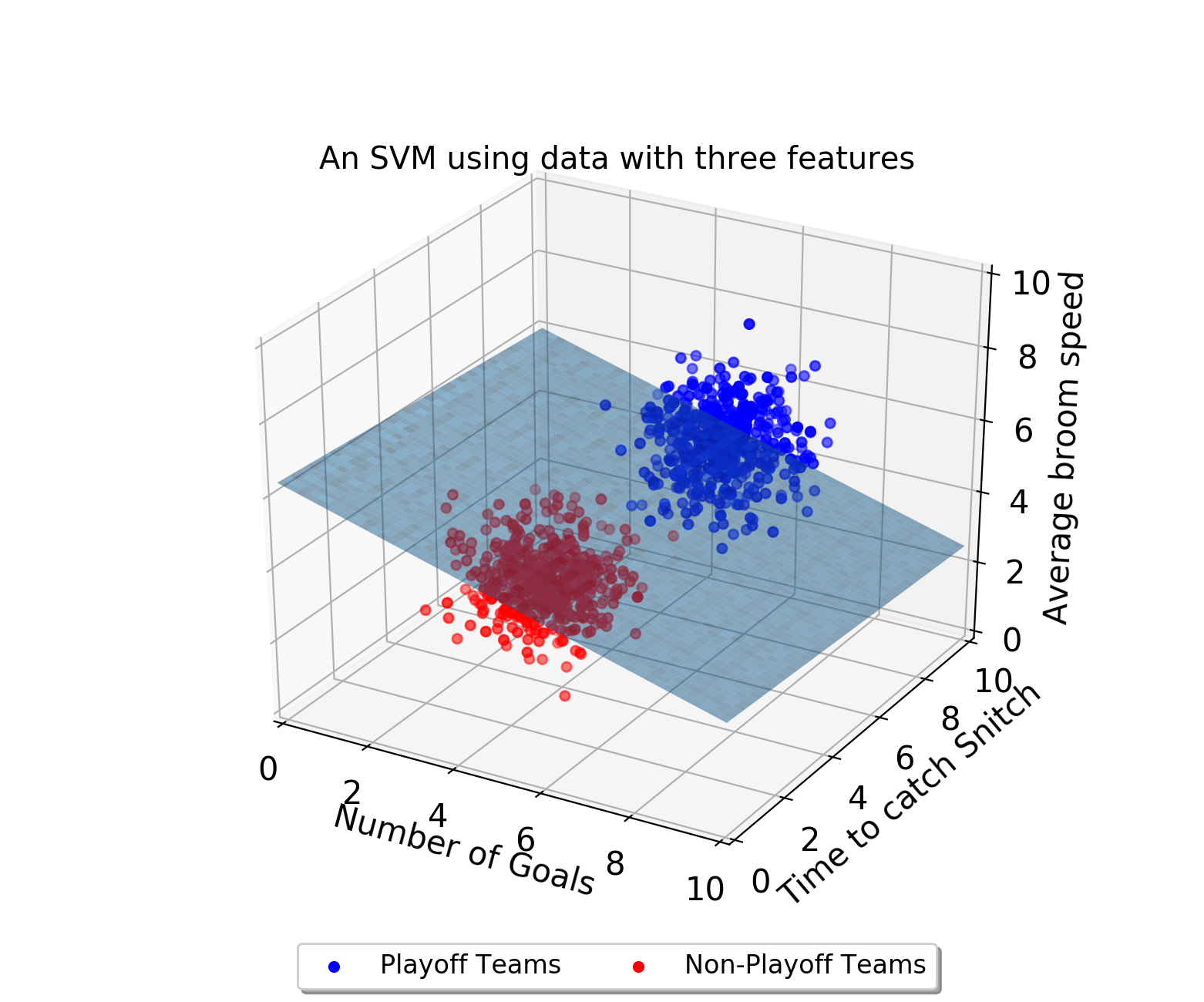
참고로 차원의 수가 이보다 더 늘어남으로써 평면으로 나타낼 수 없는 decision boundary를 hyperplane(하이퍼플레인) 이라고 부릅니다.

Optimal Decision Boundary

SVM으로 풀어야 할 문제는 바로 ‘어떤 decision boundary를 찾아야 하는가’ 입니다. 사실, 선택할 수 있는 decision boundary로 엄청나게 많은 경우의 수가 존재할 수 있습니다. 다음 그림을 봅시다.

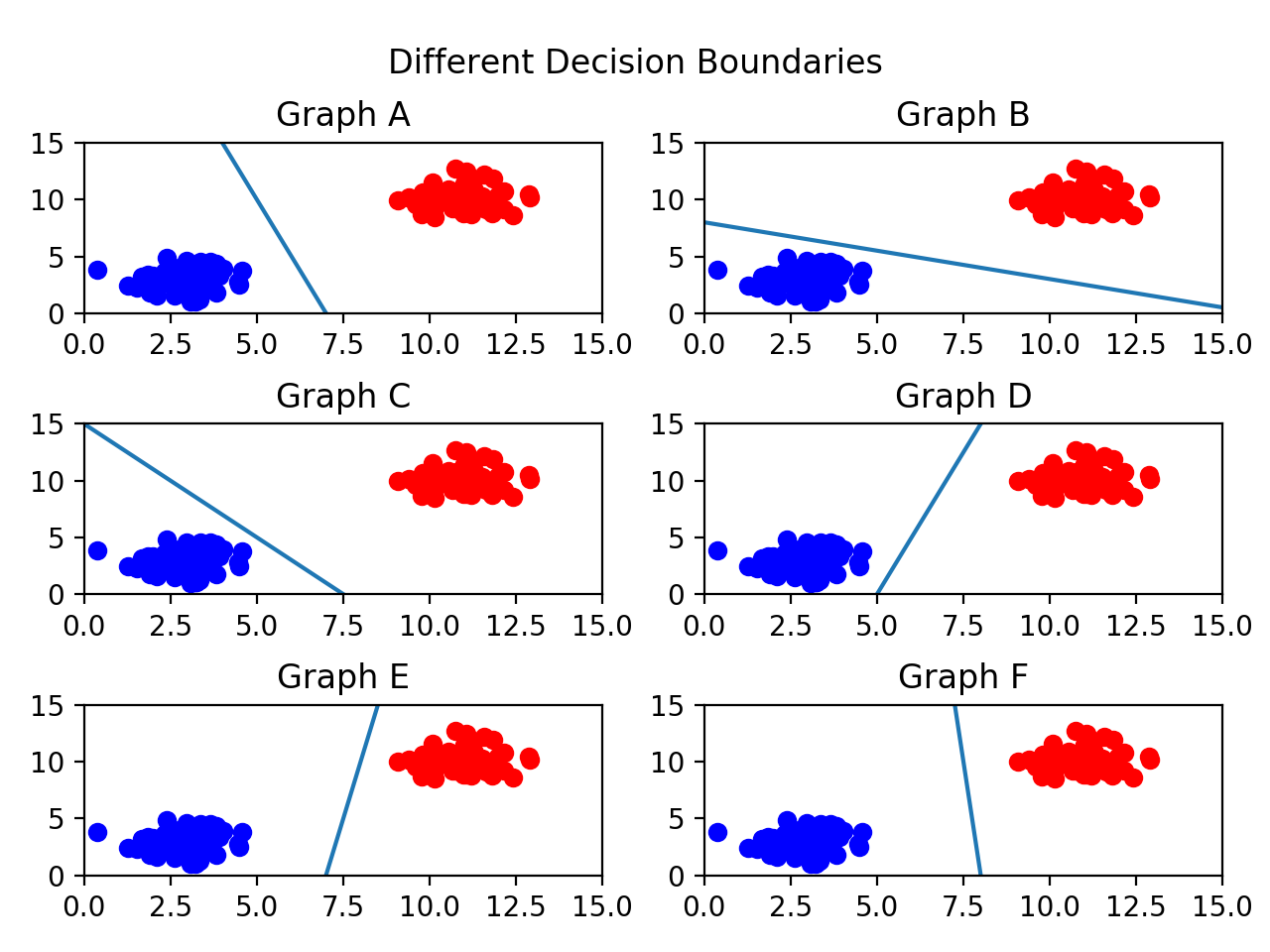
위 그림에서 나타난 decision boundary모두 데이터를 잘 분류하고 있습니다. 그러면 어떤 boundary를 선택해야 할까요? 일반적으로 두 데이터로부터 가장 멀리 떨어진 decision boundary가 가장 적합합니다. Decision boundary와 데이터간의 거리를 최대화 시키는것이 데이터를 잘못 분류할 가능성을 낮춰주기 때문입니다.

즉, 위 그림에서는 graph F가 가장 좋은 decision boundary가 될 수 있습니다.

Support Vectors and Margins

데이터들과 가장 멀리 떨어진 게 가장 좋은 decision boundary라는 사실을 알았습니다. 이러한 아이디어를 설명하는데 도움이 되는 새로운 term을 소개하겠습니다. 바로 support vectors(서포트 벡터) 입니다.

Support Vectors는 decision boundary와 가장 가까운 training set의 데이터 포인트 입니다. 사실 이 데이터 포인트들이 decision boundary를 결정합니다. 그런데 왜 vector(벡터) 라고 부르는 걸까요? 각 데이터 포인트를 좌표 공간 상에 나타냄으로써 우리는 이를 원점에서 출발하는 위치벡터로 생각해 볼 수 있습니다.

이 벡터들은 아주 중요한 역할을 하는데요, ‘support’ 라는 말에서 나오듯이 이 벡터들이 decision boundary를 결정하기 때문입니다. 만약 n 개의 feature를 사용한다면, 적어도 n+1 개의 support vectors가 존재합니다.

support vector와 decision boundary간의 거리를 margin(마진)이라고 부릅니다. 이 margin이 크면 클 수록 좋은 decision boundary가 되는 것이죠.

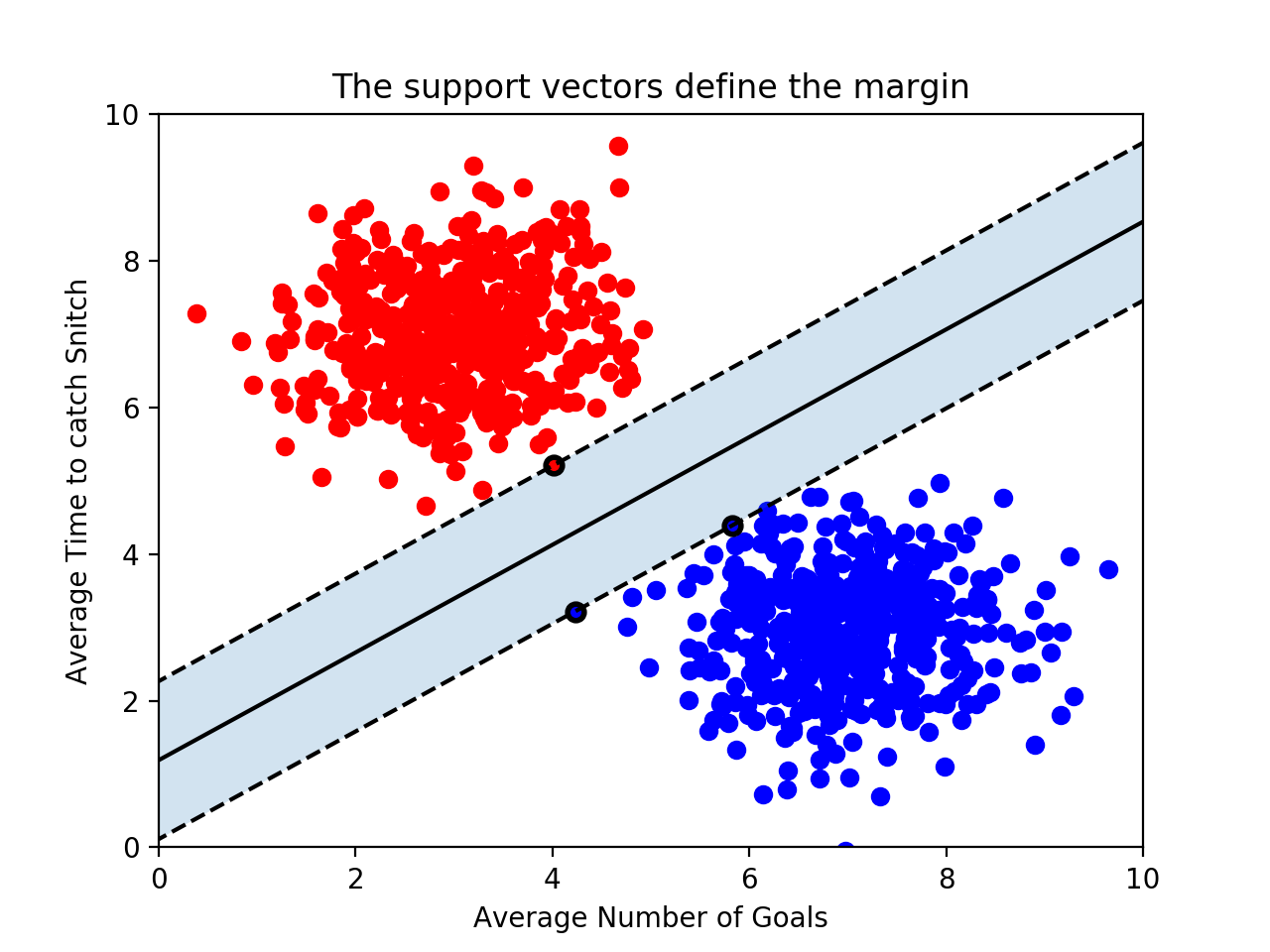
위 그림에서 support vectors를 굵은 테두리로 표시했습니다. 이 support vectors들이 decision boundary를 결정하는 결정적인 역할을 하기 때문에, 다른 training 데이터 포인트들은 무시될 수 있습니다. 이것이 바로 SVM이 가지는 강력한 장점입니다. 많은 지도 학습 모델이 predict하기 위해 모든 training 데이터를 사용하는데 비해 SVM은 support vector만 사용하면 되기 때문이죠. SVM이 빠른 이유도 여기에 있습니다.

Scikit-Learn

우리는 SVM이 어떤 원리에 의해서 margin을 최대화하는 decision boundary를 찾는지 알게 되었습니다. 그런데 최적의 decision boundary의 파라미터를 계산하는 일은 꽤 복잡한 문제입니다. 다행히, Python 라이브러리인 scikit-learn은 SVM을 활용할 수 있는 메서드를 제공합니다. 분명히 해야할 것은 최적의 decision boundary 파라미터를 계산하는 방법은 몰라도 개념적인 이해는 반드시 바탕되어야 합니다.

scikit-learn의 SVM을 사용하기 위해선 먼저 SVC 오브젝트를 생성해야 합니다. 이 때 SVC는 Support Vector Classifier 의 약자로, Support Vector Machine과 동일한 의미를 갖습니다.

from sklearn.svm import SVC

classifier = SVC(kernel = 'linear')

kernel 파라미터에 대한 설명은 조금 뒤에 하도록 하겠습니다. 다음으로, 모델을 학습시켜 줍니다. 아래의 경우 1 은 빨간색, 0 은 파란색을 나타낸다고 가정합니다.

training_points = [[1, 2], [1, 5], [2, 2], [7, 5], [9, 4], [8, 2]]
labels = [1, 1, 1, 0, 0, 0]
classifier.fit(training_points, labels)

.fit() 메서드를 호출하면 다음과 같은 decision boundary를 그립니다.

마지막으로, 새롭게 주어지는 데이터 포인트를 예측하도록 합시다. .predict() 메서드로 새로운 데이터 포인트를 전달하면 됩니다. 주의해야 할 것은 반드시 배열을 전달해야 한다는 것입니다. 단 하나의 배열을 전달하더라도 말이죠.

print(classifier.predict([[3, 2]]))

위 코드는 unclassified된 데이터 포인트 [3, 2] 가 어느 boundary에 속하는지를 예측합니다. 아래 그림은 해당 데이터 포인트를 검은색 점으로 나타냈습니다.

위 그림에서 빨간 데이터가 속한 boundary에 더 가깝기 떄문에 해당 데이터 포인트는 빨간색으로 예측될 것입니다.

SVM 모델은 .support_vectors_ 라는 내장 속성으로 support vectors의 좌표를 갖습니다. 위 경우 이를 출력하면 다음과 같은 결과를 확인할 수 있습니다.

print(classifier.support_vectors_)
# [[7, 5],
#  [8, 2],
#  [2, 2]]

Outliers

SVM은 margin을 최대화시키려고 하기 때문에 outliers(이상치)의 영향을 받게 됩니다. 다음 그림을 봅시다.

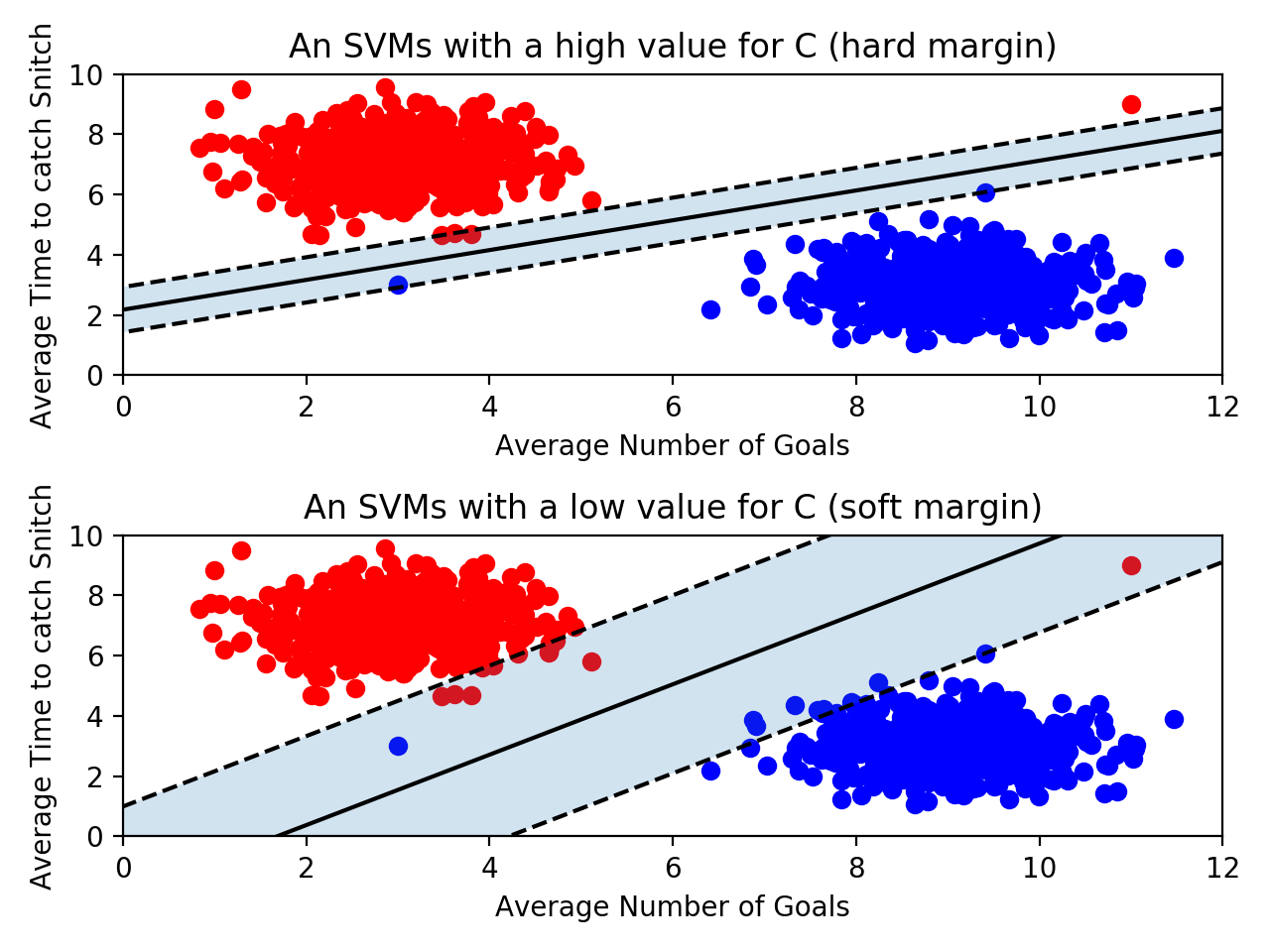
위쪽 그래프에서 파란색 데이터가 빨간 데이터 포인트에 가깝게 위치함으로써 margin이 많이 줄어들었습니다. 결과적으로 decision boundary에 영향을 미치게 되었습니다. 그러나 dicision boundary가 적당한 error을 갖도록 허용함으로써 이러한 문제를 해결할 수 있습니다.

SVM모델은 C 파라미터를 입력받을 수 있는데, 이는 SVM에게 얼마나 error을 허용할 것인지를 나타냅니다. 만약 C 값이 크다면 SVM은 hard한 margin을 보유하게 됩니다. 즉, dicision boundary가 error를 갖는 것을 강하게 제한함으로써 작은 margin을 갖게 됩니다. C 값이 너무 크다면, 해당 모델은 overfitting(오버피팅)될 수 있습니다. 즉, decision boundary가 이상치에 의해서 만들어 질 수 있습니다.

반면에 C 값이 작으면 SVM은 soft한 margin을 보유하게 됩니다. 즉, dicision boundary가 error를 갖는 것을 약하게 제한함으로써 큰 margin을 갖게 됩니다. 이 경우 이상치에 영향을 덜 받게 됩니다. 그러나 C 값이 너무 작다면 너무 많은 error를 갖게 되어 underfitting(언더피팅)될 수 있습니다.

scikit-learn을 활용하여 SVM을 만들 때 다음과 같이 C 값을 설정할 수 있습니다.

classifier = SVC(C = 0.01)

최적의 C 값은 사실 데이터에 달려 있습니다. 즉, 여러 C 값으로 모델을 평가해보면서 최적의 C 값을 찾아야 합니다.

Kernels

지금까진 선형적으로 분리될 수 있는 데이터를 예로 들었습니다. 즉 decision boundary를 직선으로 나타낼 수 있었습니다. 그런데 두 데이터를 선형적으로 분리할 수 없는 경우는 SVM을 어떻게 적용할 수 있을까요?

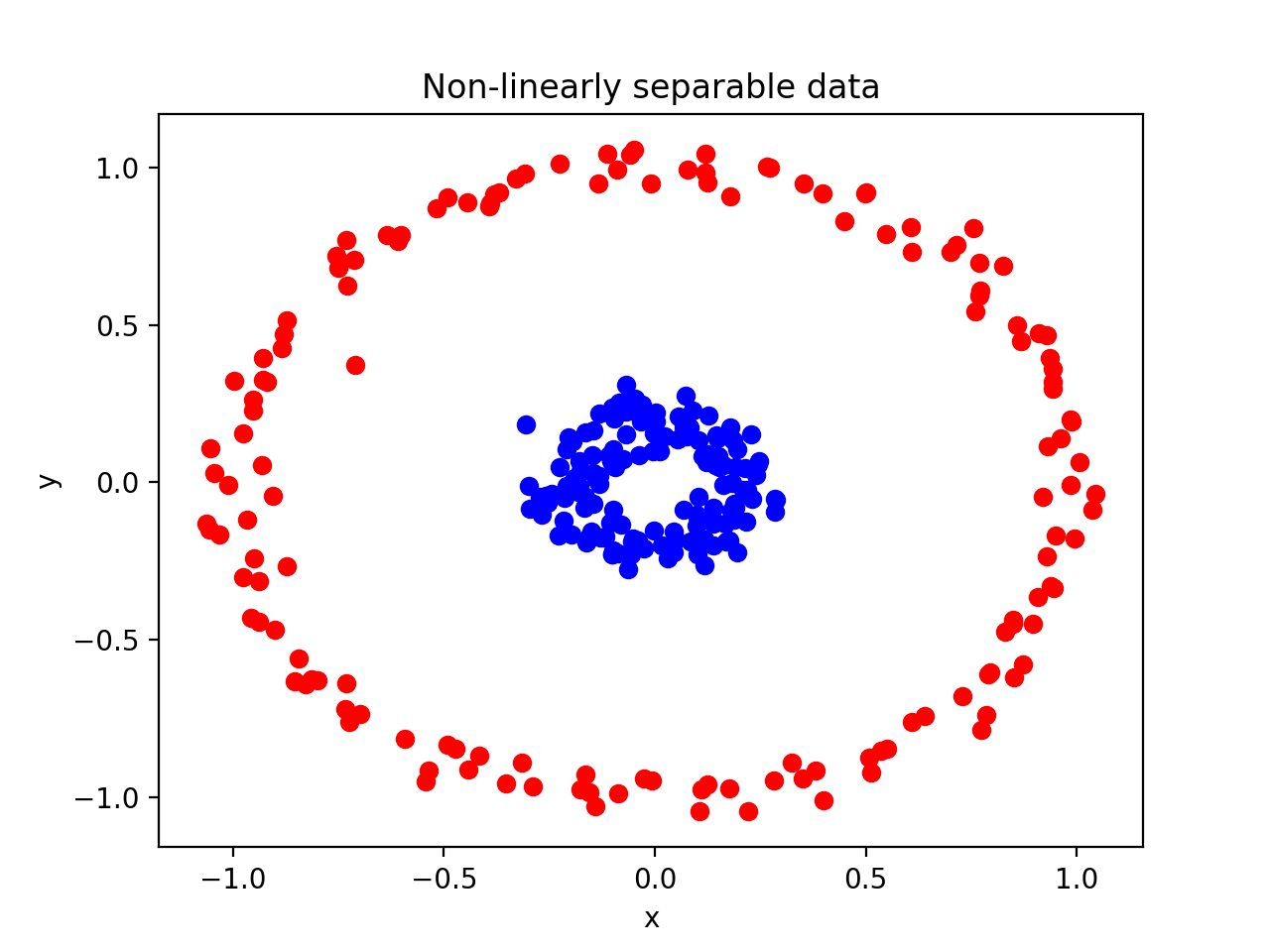
위 경우는 두 데이터의 decision boundary를 직선으로 나타낼 수 없습니다. 하지만 다행히 SVM은 이러한 데이터에서도 decision boundary를 그릴 수 있습니다. 위에서 SVM모델을 생성할 때 kernel = linear 란 옵션을 부여한것을 기억하시죠? 이 kernel이 바로 비선형적인 decision boundary를 그릴 수 있는 키 파라미터 입니다.

Polynomial Kernel

위에서 제시한 Non-linearly separable data를 다시 들여다 봅시다. 만약 SVM모델을 생성할 때 kernel 파라미터 "poly"로 설정한다면, 해당 커널은 모든 데이터 포인트를 다음과 같은 방법으로 transform 합니다.

$(x, y) \rightarrow (\sqrt{2} \cdot {x} * \cdot{y}, x^2, y^2)$

즉, 새로운 차원을 생성하게 됩니다. 예를 들어 위 kernel은 [1, 2] 를 다음과 같이 변형합니다.

$(1, 2) \rightarrow (2\sqrt2, 1, 4)$

이렇게 데이터 포인트를 변형하게 되면 위에서 제시한 Non-linearly separable data는 다음과 같이 나타낼 수 있습니다.

위 그래프에서 모든 파란색 데이터 포인트들이 빨간 데이터 포인트로부터 구분지어지는 것을 확인할 수 있습니다. 이처럼 데이터를 한 차원 위의 공간으로 projection 함으로써, 두 데이터를 선형적으로 분리할 수 있는 평면을 만들 수 있게 되었습니다.

Radial Bias Function Kernel

가장 흔하게 사용되는 SVM kernel은 바로 rbf kernel입니다. 이는 디폴트 kernel로 kernel 옵션을 따로 "linear" 이나 "poly" 로 명시하지 않는다면 자동적으로 rbf 로 설정됩니다. rbf 커널이 데이터 포인트를 어떻게 transform하는지를 시각화하는것은 꽤 복잡합니다. 위에서 사용한 polynomial kernel은 2차원 데이터를 3차원 공간상으로 변형하였지만 rbf kernel은 2차원 데이터를 무한한 차원의 공간상으로 변형하기 때문입니다.

rbf kernel이 데이터를 transform하는 것은 복잡해서 여기서 다루진 않겠지만, rbf 커널을 사용할 때 정의하는 gamma 파라미터를 이해하는 것은 중요합니다.

classifier = SVC(kernel = "rbf", gamma = 0.5, C = 2)

gamma 파라미터는 C 파라미터와 비슷합니다. gamma 값이 크면 training 데이터에 더 많은 중요도를 부여함으로써 overfitting될 수 있고, 반대로 gamma 값이 작으면 데이터에 중요도를 덜 부여함으로써 underfitting될 수 있습니다.

Review

지금까지 SVM에 대한 개념적인 이해와 scikit-learn을 사용하여 어떻게 SVM모델을 구현하는지, 그리고 SVM에서 kernel의 역할은 무엇인지 알아보았습니다. 이번 포스팅에서 배운 내용을 정리하면 다음과 같습니다.

• SVMs are supervised machine learning models used for classification.
• An SVM uses support vectors to define a decision boundary. Classifications are made by comparing unlabeled points to that decision boundary.
• Support vectors are the points of each class closest to the decision boundary. The distance between the support vectors and the decision boundary is called the margin.
• SVMs attempt to create the largest margin possible while staying within an acceptable amount of error.
• The C parameter controls how much error is allowed. A large C allows for little error and creates a hard margin. A small C allows for more error and creates a soft margin.
• SVMs use kernels to classify points that aren’t linearly separable.
• Kernels transform points into higher dimensional space. A polynomial kernel transforms points into three dimensions while an rbf kernel transforms points into infinite dimensions.
• An rbf kernel has a gammaparameter. If gamma is large, the training data is more relevant, and as a result overfitting can occur.

References

• Codecademy